Part 6 Advanced topics

6.1 Misclassified states

In the CAV example, the true state of disease is measured with error. We allowed backwards transitions to less severe disease states, though those are artefacts of misclassification and not clinically plausible.

msm can fit a Markov model to the latent true states, while estimating the error rates of the screening test that measures the disease state. This enables a more plausible model to be fitted which does not allow backwards transitions.

See ematrix argument to msm. For further details and worked examples, see the package vignette, Sections 1.6 and 2.14.

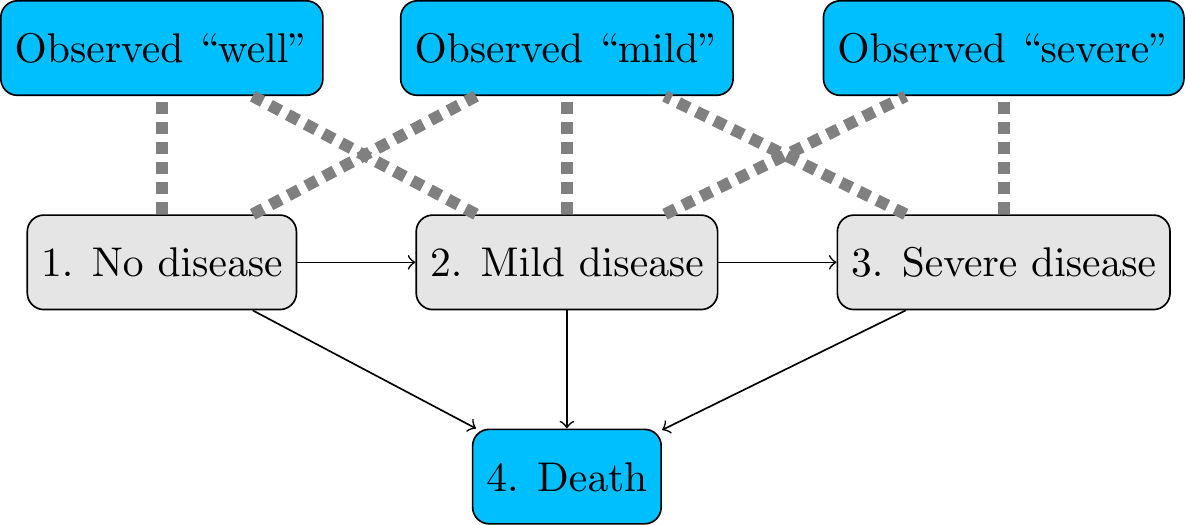
Hidden Markov multi-state model where states 1,2,3 can be misclassified

Figure 6.1: Hidden Markov multi-state model where states 1,2,3 can be misclassified

6.2 General hidden Markov models

In msm we can have an outcome of any kind that is generated conditionally on a hidden disease state. We specify

  • a continuous-time Markov model for the hidden state

  • a model for the distribution of the outcome given the hidden state (e.g. normal, binomial, Poisson…). We can even have multiple outcomes generated conditionally independently given the same hidden state.

Examples: one or more symptoms of a disease are observed intermittently, which together indicate clinically-meaningful presence/absence of a disease.

See hmodel argument to the msm function.

For further details and worked examples, see the package vignette, Sections 1.6 and 2.18.

For an example with multiple outcomes in psoriatic arthritis, see. e.g. Jackson et al..

6.3 Semi-Markov models

In a Markov model, the time to the next state does not depend on how long you have spent in that state. Relaxing that assumption is tricky if the data are intermittently observed, because the time of state entry is unknown.

6.3.1 “phase-type” semi-Markov model

To relax the Markov assumption for a specific state, split up that state into hidden “phases” and define a Markov model on a state space defined by the phases and the remaining states. Transition time between the phases is unknown. For example:

Phase-type semi-Markov model

Figure 6.2: Phase-type semi-Markov model

This is equivalent to making the sojourn distribution in state 2 more flexible than an exponential distribution, so the hazard of leaving state 2 depends on how long has been spent there.

It is a (partially) hidden Markov model, hence can be implemented in msm using its hidden Markov model machinery.

See the phase.states option to the msm function.

The idea is from Titman and Sharples, but it hasn’t been applied much in practice.

6.4 Some things that msm can’t do

Random effects (frailty) multi-state models for intermittently-observed data

  • Theoretically possible in JAGS, Stan or BUGS (Bayesian approach), though requires writing out a model likelihood in the program’s own language. Some examples in van den Hout (2017).

  • Several R packages available for random effects models with time-to-event data - e.g. frailtypack and others in the CRAN task view.

Models with informative sampling times (e.g. person is more likely to be observed at times when their disease is more severe.) See e.g.