Cumulative intensity function for parametric multi-state models

Cumulative transition-specific intensity/hazard functions for fully-parametric multi-state or competing risks models, using a piecewise-constant approximation that will allow prediction using the functions in the mstate package.

Usage

msfit.flexsurvreg(
  object,
  t,
  newdata = NULL,
  variance = TRUE,
  tvar = "trans",
  trans,
  B = 1000
)

Arguments

object

Output from flexsurvreg or flexsurvspline, representing a fitted survival model object.

The model should have been fitted to data consisting of one row for each observed transition and additional rows corresponding to censored times to competing transitions. This is the "long" format, or counting process format, as explained in the flexsurv vignette.

The model should contain a categorical covariate indicating the transition. In flexsurv this variable can have any name, indicated here by the tvar argument. In the Cox models demonstrated by mstate it is usually included in model formulae as strata(trans), but note that the strata function does not do anything in flexsurv. The formula supplied to flexsurvreg should be precise about which parameters are assumed to vary with the transition type.

Alternatively, if the parameters (including covariate effects) are assumed to be different between different transitions, then a list of transition-specific models can be formed. This list has one component for each permitted transition in the multi-state model. This is more computationally efficient, particularly for larger models and datasets. See the example below, and the vignette.

t

Vector of times. These do not need to be the same as the observed event times, and since the model is parametric, they can be outside the range of the data. A grid of more frequent times will provide a better approximation to the cumulative hazard trajectory for prediction with probtrans or mssample, at the cost of greater computational expense.

newdata

A data frame specifying the values of covariates in the fitted model, other than the transition number. This must be specified if there are other covariates. The variable names should be the same as those in the fitted model formula. There must be either one value per covariate (the typical situation) or \(n\) values per covariate, a different one for each of the \(n\) allowed transitions.

variance

Calculate the variances and covariances of the transition cumulative hazards (TRUE or FALSE). This is based on simulation from the normal asymptotic distribution of the estimates, which is computationally-expensive.

tvar

Name of the categorical variable in the model formula that represents the transition number. This should have been defined as a factor, with factor levels that correspond to elements of trans, conventionally a sequence of integers starting from 1. Not required if x is a list of transition-specific models.

trans

Matrix indicating allowed transitions in the multi-state model, in the format understood by mstate: a matrix of integers whose \(r,s\) entry is \(i\) if the \(i\)th transition type (reading across rows) is \(r,s\), and has NAs on the diagonal and where the \(r,s\) transition is disallowed.

B

Number of simulations from the normal asymptotic distribution used to calculate variances. Decrease for greater speed at the expense of accuracy.

Value

An object of class "msfit", in the same form as the objects used in the mstate package. The msfit method from mstate returns the equivalent cumulative intensities for Cox regression models fitted with coxph.

References

Liesbeth C. de Wreede, Marta Fiocco, Hein Putter (2011). mstate: An R Package for the Analysis of Competing Risks and Multi-State Models. Journal of Statistical Software, 38(7), 1-30. doi:10.18637/jss.v038.i07

Mandel, M. (2013). "Simulation based confidence intervals for functions with complicated derivatives." The American Statistician 67(2):76-81

Author

C. H. Jackson chris.jackson@mrc-bsu.cam.ac.uk

Examples


## 3 state illness-death model for bronchiolitis obliterans
## Compare clock-reset / semi-Markov multi-state models

## Simple exponential model (reduces to Markov)

bexp <- flexsurvreg(Surv(years, status) ~ trans,
                    data=bosms3, dist="exp")
tmat <- rbind(c(NA,1,2),c(NA,NA,3),c(NA,NA,NA))
mexp <- msfit.flexsurvreg(bexp, t=seq(0,12,by=0.1),
                          trans=tmat, tvar="trans", variance=FALSE)

## Cox semi-parametric model within each transition

bcox <- coxph(Surv(years, status) ~ strata(trans), data=bosms3)

if (require("mstate")){

mcox <- mstate::msfit(bcox, trans=tmat)

## Flexible parametric spline-based model 

bspl <- flexsurvspline(Surv(years, status) ~ trans + gamma1(trans),
                       data=bosms3, k=3)
mspl <- msfit.flexsurvreg(bspl, t=seq(0,12,by=0.1),
                         trans=tmat, tvar="trans", variance=FALSE)

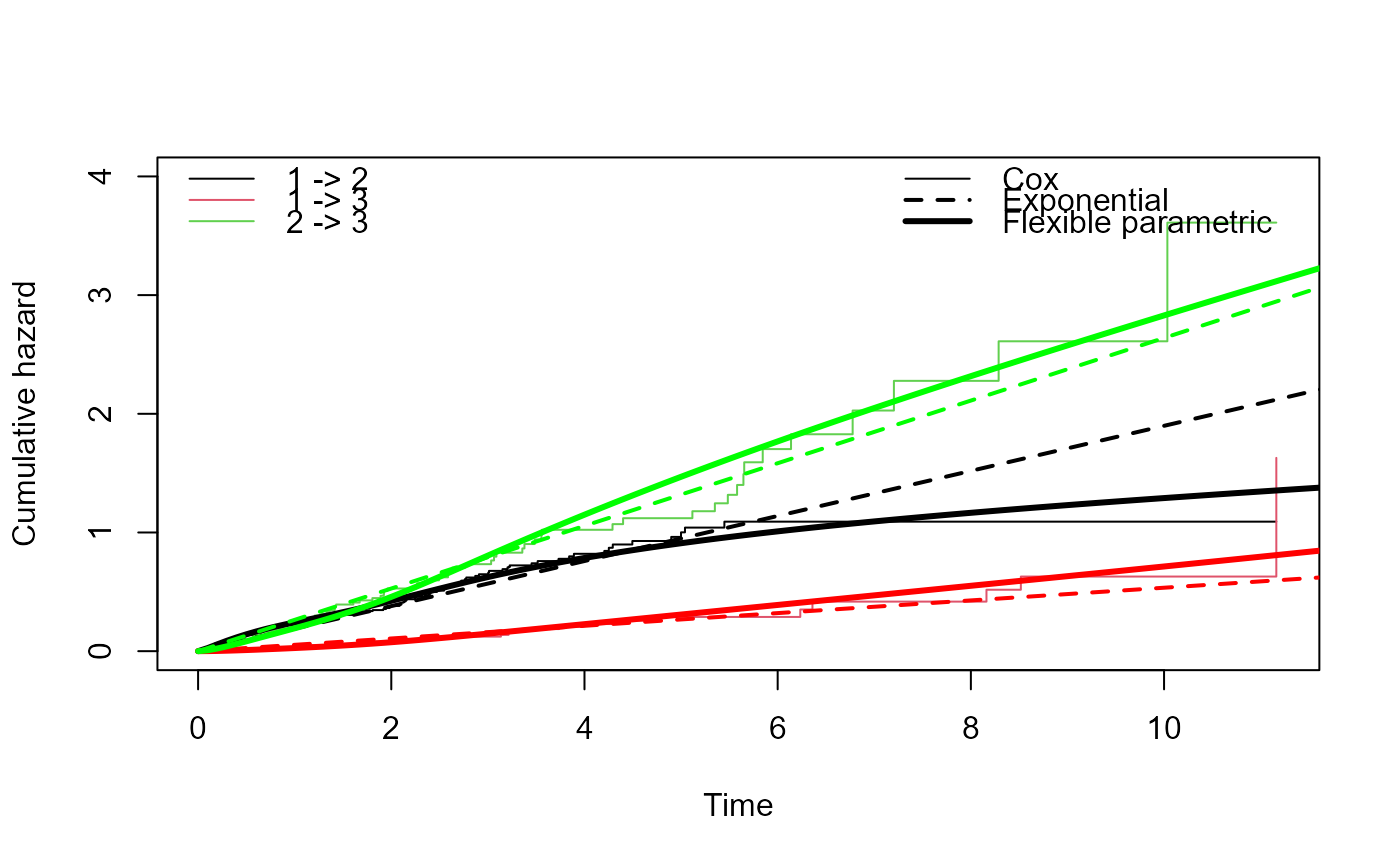
## Compare fit: exponential model is OK but the spline is better

plot(mcox, lwd=1, xlim=c(0, 12), ylim=c(0,4))
cols <- c("black","red","green")
for (i in 1:3){
    lines(mexp$Haz$time[mexp$Haz$trans==i], mexp$Haz$Haz[mexp$Haz$trans==i],
             col=cols[i], lwd=2, lty=2)
    lines(mspl$Haz$time[mspl$Haz$trans==i], mspl$Haz$Haz[mspl$Haz$trans==i],
             col=cols[i], lwd=3)
}
legend("topright", lwd=c(1,2,3), lty=c(1,2,1),
   c("Cox", "Exponential", "Flexible parametric"), bty="n")

}
#> Loading required package: mstate


## Fit a list of models, one for each transition
## More computationally efficient, but only valid if parameters
## are different between transitions.

if (FALSE) {
bexp.list <- vector(3, mode="list")
for (i in 1:3) { 
  bexp.list[[i]] <- flexsurvreg(Surv(years, status) ~ 1, subset=(trans==i),
                                data=bosms3, dist="exp")
}

## The list of models can be passed to this and other functions,
## as if it were a single multi-state model. 

msfit.flexsurvreg(bexp.list, t=seq(0,12,by=0.1), trans=tmat)
}