Nonparametric estimator of survival from right-truncated, uncensored data

Estimates the survivor function from right-truncated, uncensored data by reversing time, interpreting the data as left-truncated, applying the Kaplan-Meier / Lynden-Bell estimator and transforming back.

Usage

survrtrunc(t, rtrunc, tmax, data = NULL, eps = 0.001, conf.int = 0.95)

Arguments

t: Vector of observed times from an initial event to a final event.
rtrunc: Individual-specific right truncation points, so that each individual's survival time t would not have been observed if it was greater than the corresponding element of rtrunc. If any of these are greater than tmax, then the actual individual-level truncation point for these individuals is taken to be tmax.
tmax: Maximum possible time to event that could have been observed.
data: Data frame to find t and rtrunc in. If not supplied, these should be in the working environment.
eps: Small number that is added to t before implementing the time-reversed estimator, to ensure the risk set is consistent between forward and reverse time scales. It should be just large enough that t+eps is not ==t. This should not need changing from the default of 0.001, unless t are extremely large or small and the data are rounded to integer.
conf.int: Confidence level, defaulting to 0.95.

Value

A list with components:

time Time points where the estimated survival changes.

surv Estimated survival at time, truncated above at

tmax.

se.surv Standard error of survival.

std.err Standard error of -log(survival). Named this way for consistency with survfit.

lower Lower confidence limits for survival.

upper Upper confidence limits for survival.

Details

Note that this does not estimate the untruncated survivor function - instead it estimates the survivor function truncated above at a time defined by the maximum possible time that might have been observed in the data.

Define \(X\) as the time of the initial event, \(Y\) as the time of the final event, then we wish to determine the distribution of \(T = Y- X\).

Observations are only recorded if \(Y \leq t_{max}\). Then the distribution of \(T\) in the resulting sample is right-truncated by rtrunc \( = t_{max} - X\).

Equivalently, the distribution of \(t_{max} - T\) is left-truncated, since it is only observed if \(t_{max} - T \geq X\). Then the standard Kaplan-Meier type estimator as implemented in survfit is used (as described by Lynden-Bell, 1971) and the results transformed back.

This situation might happen in a disease epidemic, where \(X\) is the date of disease onset for an individual, \(Y\) is the date of death, and we wish to estimate the distribution of the time \(T\) from onset to death, given we have only observed people who have died by the date \(t_{max}\).

If the estimated survival is unstable at the highest times, then consider replacing tmax by a slightly lower value, then if necessary, removing individuals with t > tmax, so that the estimand is changed to the survivor function truncated over a slightly narrower interval.

References

D. Lynden-Bell (1971) A method of allowing for known observational selection in small samples applied to 3CR quasars. Monthly Notices of the Royal Astronomical Society, 155:95–118.

Seaman, S., Presanis, A. and Jackson, C. (2020) Review of methods for estimating distribution of time to event from right-truncated data.

Examples


## simulate some event time data
set.seed(1)
X <- rweibull(100, 2, 10)
T <- rweibull(100, 2, 10)

## truncate above
tmax <- 20
obs <- X + T < tmax
rtrunc <- tmax - X
dat <- data.frame(X, T, rtrunc)[obs,]
sf <-    survrtrunc(T, rtrunc, data=dat, tmax=tmax)
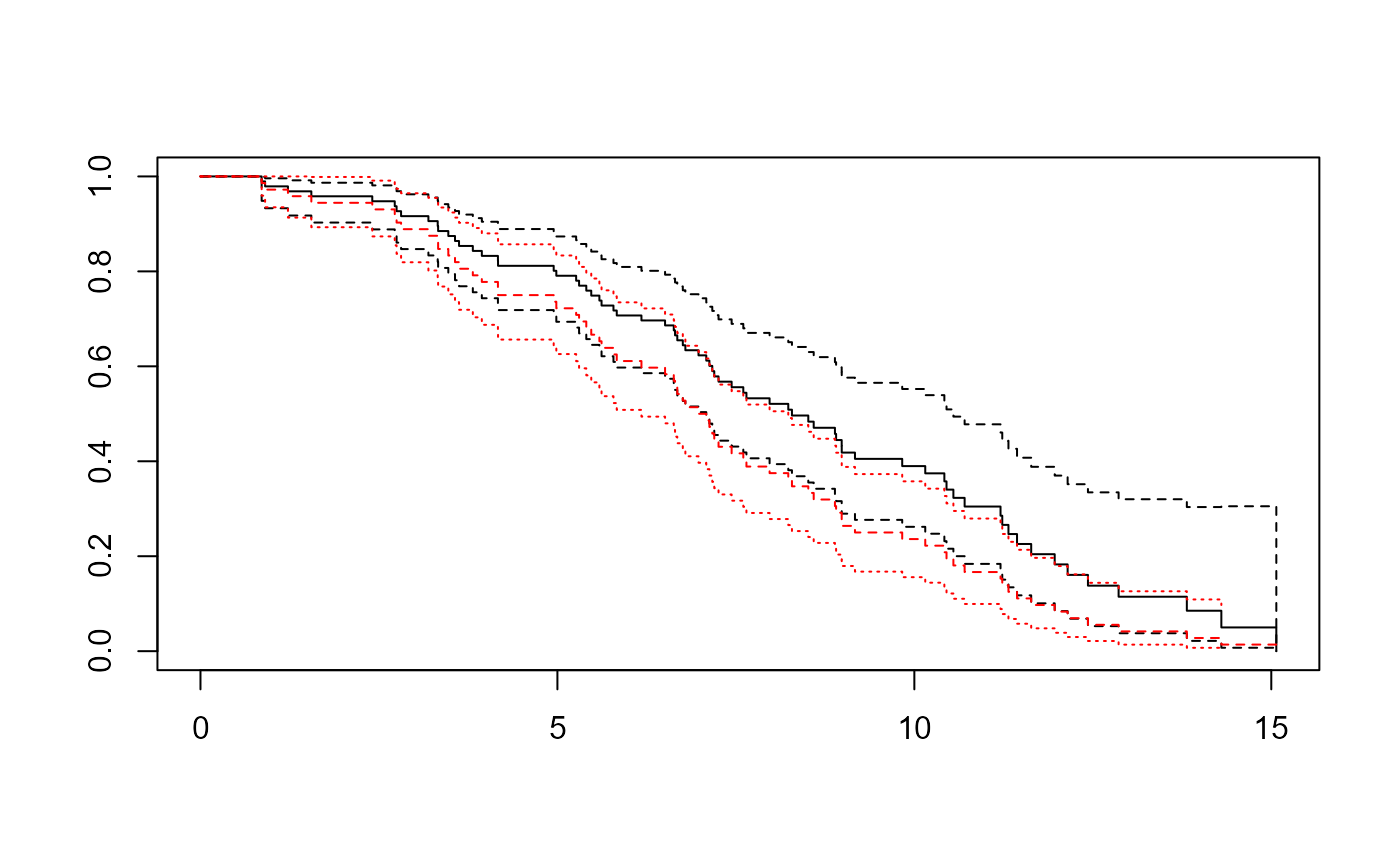
plot(sf, conf.int=TRUE)
## Kaplan-Meier estimate ignoring truncation is biased
sfnaive <- survfit(Surv(T) ~ 1, data=dat)
lines(sfnaive, conf.int=TRUE, lty=2, col="red")


## truncate above the maximum observed time
tmax <- max(X + T) + 10
obs <- X + T < tmax
rtrunc <- tmax - X
dat <- data.frame(X, T, rtrunc)[obs,]
sf <-    survrtrunc(T, rtrunc, data=dat, tmax=tmax)
plot(sf, conf.int=TRUE)
## estimates identical to the standard Kaplan-Meier
sfnaive <- survfit(Surv(T) ~ 1, data=dat)
lines(sfnaive, conf.int=TRUE, lty=2, col="red")